Producto escalar y vectorial
| PRODUCTO ENTRE VECTORES (multiplicación entre vectores)Por el contrario que los escalares, los vectores pueden multiplicarse de dos maneras diferentes: producto escalar y producto vectorial. El producto escalar es una operación de multiplicar dos vectores cuyo resultado deja de ser un vector: el producto se transforma en un escalar (un número más su unidad si correspondiera). El producto vectorial es una operación diferente a la anterior, y el resultado es un nuevo vector que tiene todas las características de los vectores. | ||||
| Producto escalar | ||||
Dos vectores cualesquiera (por ejemplo uno que representa una fuerza y otro que representa un desplazamiento) se pueden multiplicar entre sí de esta manera.A . B = cDonde A es un vector, B es el otro vector y c es el resultado: un escalar. La operación se puede realizar de dos maneras (absolutamente equivalentes). Modo uno, conociendo los módulos de los vectores A y B, y , α, el ángulo que forman entre sí. A . B = |A| . |B| . cos α = cFijate que todo se resume a un producto entre 3 escalares, ya que los módulos de los vectores -|A| y |B|- son escalares, y los cosenos ídem. Luego, el resultado, c, no puede ser otra cosa que un escalar. El segundo modo, equivalente al primero, lo usás cuando no conocés el ángulo que forman los vectores que vas a multiplicar escalarmente ni sus módulos... pero conocés las componentes (o proyecciones) de cada vector: A = ax î + ay ĵ + az kFijate que se trata de la suma de dos productos entre dos escalares (las componentes sin los versores), de modo que el resultado debe ser un escalar. Mirá este ejemplo muy usado en Física Elemental: | ||||
| ||||
| Producto vectorial | ||||
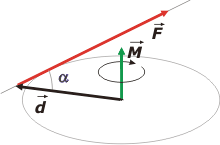
Dos vectores cualesquiera (por ejemplo uno que representa una velocidad angular y otro que representa una posición) se pueden multiplicar entre sí de esta manera.A x B = VDonde A es un vector, B es el otro vector y V es el resultado: un nuevo vector. La operación se puede realizar de dos maneras (absolutamente equivalentes). Modo uno, conociendo los módulos de los vectores A y B, y , α, el ángulo que forman entre sí. A x B = |A| . |B| . sen α . û = VDonde V es el vector resultado de la operación y cuya dirección es perpendicular al plano que forman A y B, y el sentido está señalado por el dedo pulgar de la mano derecha, el índice al primer vector y el mayor al segundo (el producto vectorial no es conmutativo: A x B = − (B x A). Y û es un versor que tiene la dirección y sentido de V (puesto ahí justamente para darle carácter vectorial a esa operación). El segundo modo, equivalente al primero, lo usás cuando no conocés el ángulo que forman los vectores que vas a multiplicar vectorialmente ni sus módulos... pero conocés las componentes (o proyecciones) de cada vector: A = ax î + ay ĵ + az kA x B = (aybz – azby) î + (azbx – axbz) ĵ + (axby – aybx) k = V Te lo hago más simple: |A x B| = (aybz – azby ; azbx – axbz ; axby – aybx) = |V| Así encontramos el módulo del vector buscado y la dirección y sentido la sacás con la regla de la mano derecha (eso te indica el resultado del producto vectorial depende del sistema de referenica -en este caso terna de ejes- que uses). Mirá este otro ejemplo: | ||||
|

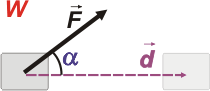
0 comentarios: