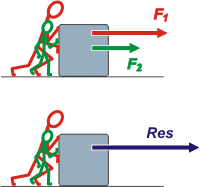Suma de vectores, Resultante

Si dos personas hacen fuerzas en la misma dirección y sentido, sus fuerzas se suman. Los vectores que representan sus fuerzas también se suman y el resultado de esa suma se denomina Resultante, Res. En este caso, la resultante tiene la misma dirección y sentido que las fuerzas originales y su módulo es igual a la suma de ellos. Res  =  F1 + F2 ΣF = F1 + F2
Por ejemplo, si el grande empuja con una fuerza de 15 kgf y el chico con una fuerza de 8 kgf, la cosa funciona como si hubiese una sola persona empujando con una fuerza de 23 kgf . (23 = 15 + 8)
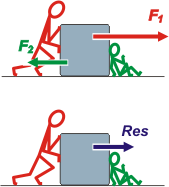Si dos personas hacen fuerzas en la misma dirección pero con sentidos opuestos la resultante tendrá la misma dirección de ambas, el sentido de la más grande (módulo mayor) y su módulo será igual a la resta entre los módulos ΣF = Res  =  F1 – F2 Fíjate que la operación sigue llamándose suma. Y la resultante se sigue llamando sumatoria
Por ejemplo, si el grande empuja con una fuerza de 15 kgf y el chico resiste con una fuerza de 8 kgf, la cosa funciona como si hubiese una sola persona empujando con una fuerza de 7 kgf . (7 = 15 – 8).
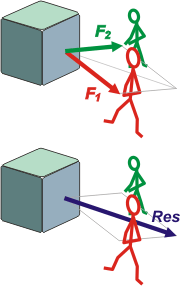Imagínate que dos personas tiran de una caja con sogas. Ambos tiran con fuerzas de distinta intensidad, y también, con distintas direcciones. La caja reacciona como si una sola soga estuviera tirando de ella, es la fuerzas resultante, que tendrá una dirección intermedia y un módulo que se puede obtener gráfica o analíticamente... y hay que aprender ambas modalidades. Pero voy a destacar que la suma de vectores, salvo en los casos unidireccionales que te comenté arriba, no ocurre alegremente como si de números se tratara. Por ejemplo en nuestro caso el tipo rojo puede estar haciendo una fuerza de F1 = 15 kgf (la roja), el otro una de F2 = 8 kgf (la verde), y la resultante, o sea, la suma de ambas (que representé en azul) puede valer, digamos, 19 kgf , dependiendo del ángulo que forman F1 con F2.
Las operaciones con vectores (suma, resta y multiplicación) son necesarias para este curso. Al conjunto de operaciones se lo llama álgebra vectorial. En las páginas siguientes vas a encontrar el álgebra vectorial necesaria para este curso de física.